¿Qué es el Mapa de Karnaugh?
El mapa
de Karnaugh o mapa-k es un diagrama utilizado para la simplificación de
funciones algebraicas Booleanas, permitiendo de manera gráfica reconocer
patrones y así reduce la necesidad de hacer cálculos extensos para la simplificación
de expresiones booleanas.
Ventajas del Mapa de Karnaugh
• El
mapa-k nos permite convertir la tabla de verdad de una ecuación booleana en una
forma SOP minimizada
• Reglas
básicas y sencillas para la simplificación.
• La
facilidad del método permite que sea más rápido y más eficiente que otras
técnicas de simplificación en el Álgebra de Boole.
1. Las
agrupaciones o el término a considerar únicamente será del número “1”.
2. Las
agrupaciones únicamente se deben hacer en horizontal y vertical.
3. Las
agrupaciones a considerar deben contener 2n elementos. Es decir cada agrupación
que contiene cada grupo tendrá 1, 2, 4,8,…, 2n cantidad de número de uno o
unos.
4. Para
una mejor simplificación se debe considerar el grupo más grande posible.
5. Se
debe considerar todo número “1”.
6. Es
posible solapar grupos de “1”
7. La
formación de grupos también se pueden producir con las celdas extremas de la
tabla.
8.
Debemos considerar el menor número de agrupaciones o grupos posibles
obedeciendo las reglas anteriores.
Aplicaciones
Los
diagramas de Karnaugh pueden ser utilizados en la simplificación de sentencias
definidas en lógica Booleana, construcción de estaciones de clasificación,
selección y control de calidad de piezas fabricadas, entre otras aplicaciones
El mapa
de Karnaugh o diagrama de Karnaugh (también conocido como tabla de Karnaugh o
diagrama de Veitch, abreviado como K-Mapa o KV-Mapa) fue inventado en 1950 por
Maurice Karnaugh, físico y matemático de los laboratorios Bell.
El mapa
de Karnaugh es uno de los métodos utilizados para la minimización de funciones
algebraicas booleanas y es utilizado también para minimizar expresiones del
tipo suma de productos o productos de sumas, obteniendo así otra suma de
productos y otros productos de sumas. La expresión obtenida será mínima.
Se
trata de una serie de cuadrados, cada cuadrado constituye una línea de la tabla
de verdad. Dicha tabla despliega el valor de verdad de una proposición
compuesta, para cada combinación de valores de verdad que se puedan establecer
a sus componentes.
Como la tabla de verdad de una función de N variables tiene 2N filas, el mapa K correspondiente debe poseer 2N cuadrados. Cada cuadrado tiene como componente un 0 ó un 1, esto depende del valor que toma la función en cada fila. Las tablas de Karnaugh pueden ser utilizadas para funciones de hasta 6 variables.
Como la tabla de verdad de una función de N variables tiene 2N filas, el mapa K correspondiente debe poseer 2N cuadrados. Cada cuadrado tiene como componente un 0 ó un 1, esto depende del valor que toma la función en cada fila. Las tablas de Karnaugh pueden ser utilizadas para funciones de hasta 6 variables.
Los
Mapas de Karnaugh sirven para obtener una función mínima de dos niveles Suma de
Productos. Una expresión de dos niveles es considerada, expresión mínima si:
1. No hay otra expresión equivalente que contenga menos productos.
2. No
hay otra expresión equivalente que conste con el mismo número de productos, con
un menor número de literales.
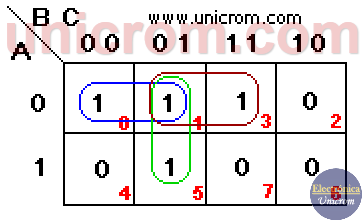
Veamos un Ejemplo:


No hay comentarios.:
Publicar un comentario