Algebra Booleana

¿Qué es el Álgebra Booleana?

     Es una rama especial del álgebra que se usa principalmente en electrónica digital. El álgebra booleana fue inventada en el año 1854 por el matemático inglés George Boole.

     El álgebra de Boole es un método para simplificar los circuitos lógicos (o a veces llamados circuitos de conmutación lógica) en electrónica digital.

     Por lo tanto, también se llama como "Cambio de álgebra". Podemos representar el funcionamiento de los circuitos lógicos utilizando números, siguiendo algunas reglas, que son bien conocidas como "Leyes del álgebra de Boole".

     También podemos hacer los cálculos y las operaciones lógicas de los circuitos aún más rápido siguiendo algunos teoremas, que se conocen como "Teoremas del álgebra de Boole". Una función booleana es una función que representa la relación entre la entrada y la salida de un circuito lógico.

     La lógica booleana sólo permite dos estados del circuito, como True y False. Estos dos estados están representados por 1 y 0, donde 1 representa el estado "Verdadero" y 0 representa el estado "Falso".

Leyes del Álgebra Booleana

Leyes Conmutativas:

     Las "Leyes Conmutativas" significan que puedes intercambiar números de cualquier manera y aun así obtener la misma respuesta cuando los sumes. O cuando los multipliques.

     En matemáticas, la propiedad conmutativa o conmutatividad es una propiedad fundamental que tienen algunas operaciones según la cual el resultado de operar dos elementos no dependen del orden en que se toman. Esto se cumple en la adición y la multiplicación ordinarias: el orden de los sumandos no altera la suma, o el orden de los factores no altera el producto.

Leyes Asociativas:

     Las "Leyes asociativas" quieren decir que no importa cómo agrupes los números (o sea, qué calculas primero) cuando sumas o cuando multiplicas.

     En una expresión asociativa con dos o más ocurrencias seguidas de un mismo operador asociativo, el orden en que se ejecuten las operaciones no altera el resultado, siempre y cuando se mantenga intacta la secuencia de los operandos. 

Leyes Distributivas:

     En matemáticas y en particular en álgebra abstracta, la distributiva es la propiedad de los operadores binarios que generaliza la propiedad distributiva del álgebra elemental.

     La propiedad distributiva de la multiplicación sobre la suma en álgebra elemental es aquella en la que el resultado de un número multiplicado por la suma de dos o más sumandos, es igual a la suma de los productos de cada uno sumando por ese número. 

Aplicación del Álgebra Booleana

     La herramienta fundamental para el análisis y diseño de circuitos digitales es el Álgebra Booleana. Esta álgebra es un conjunto de reglas matemáticas (similares en algunos aspectos al álgebra convencional), pero que tienen la virtud de corresponder al comportamiento de circuitos basados en dispositivos de conmutación (interruptores, relevadores, transistores, etc). Es posible construir circuitos digitales llamados compuertas lógicas que con diodos, transistores y resistencias conectados de cierta manera hacen que la salida del circuito sea el resultado de una operación lógica básica sobre la entrada.

Existen tres operaciones básicas: OR, AND Y NOT.

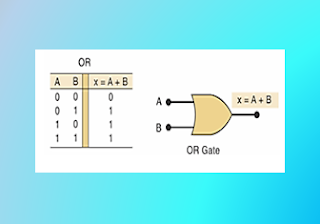
Compuerta OR:

• La salida es Verdadera si al menos una de las Entradas es Verdadera.
• La expresión booleana para la operación OR:

• La operación OR produce un resultado (salida) de 1 cuando cualquier entrada se un 1. De otra manera la salida será 0.
• Una compuerta OR es un circuito lógico que realiza una operación OR en las entradas del circuito.
• La expresión x= A + B se lee “x es igual a A OR B”. 

Compuerta AND:

• La salida es Verdadera si y solamente si todas las entradas son Verdaderas.
• La expresión booleana para la operación es:

• La operación AND se realiza igual que la multiplicación de unos y cero.
• La compuerta AND es un circuito lógico que realiza la operación AND en las entradas del circuito.
• La salida de una compuerta AND será 1 sólo para el caso en que todas las entradas sean 1; para todos los otros casos será 0.
• La expresión x = AB se lee “x es igual a A y B”.

Compuerta NOT:

• Su función es producir una salida inversa o contraria a su entrada es decir convertir unos a ceros y ceros a unos.

X=A

Compuerta NAND:

• También conocida como AND negada o inversa, es una combinación de las compuertas AND y NOT que se representa con la compuerta AND con un círculo a la salida, al tener sus entradas activas “1” la salida se encuentra inactiva “0”, otra variación con respeto a las entradas mantendrá su salida en estado activo “1”.  Se puede representar mediante un circuito con dos interruptores en serie y debemos recordar que el flujo de corriente circula por donde se tenga menor resistencia.

Compuerta NOR:

• Es una combinación de las compuertas OR y NOT, en otras palabras la compuerta NOR es la versión inversa de la compuerta OR. Al tener sus entradas en estado inactivo “0” su salida estará en un estado activo “1”, pero si alguna de las entradas pasa a un estado binario “1” su salida tendrá un estado inactivo “0”.  Se puede representar mediante un circuito con los interruptores y salida en paralelo, para tener la salida en estado activo “1” es necesario que ambos interruptores se encuentren abiertos, mientras alguno de los interruptores se encuentre cerrado la salida “y” tendrá un estado binario “0”.

Compuerta XOR:

• También conocida como “OR exclusiva”, su expresión Booleana es una suma binaria de un dígito cada uno y el resultado obtenido será la salida. La salida tiene un estado activo “1” al tener las entradas en estados diferentes (Una activa y otra inactiva). Su representación es mediante cuatro interruptores que se encuentran acoplados mecánicamente a su valor negado, de este modo cuando A se cierra entonces A´ se abre y viceversa, lo mismo ocurre con el interruptor B con respecto al B´.

Compuerta XNOR:

• Es la negación de la compuerta XOR, cuando las entradas sean iguales se representará una salida en estado “1” y si son diferentes la salida será un estado “0”.